Machine learning(ML) refers to a collection of programming techniques that allow computers to make distinctions or recognize patterns without explicit commands. This field is based on statistical methods and emerged from artificial intelligence research in the late 1950s and early 1960s. Applications of ML include optical character recognition, sentiment analysis, computer vision and prediction making. People with experience in ML are highly desired in the job market and learning based algorithms are making more and more important decisions in our society. So as an emerging programer its probably worth while to learn a bit about how machines learn.
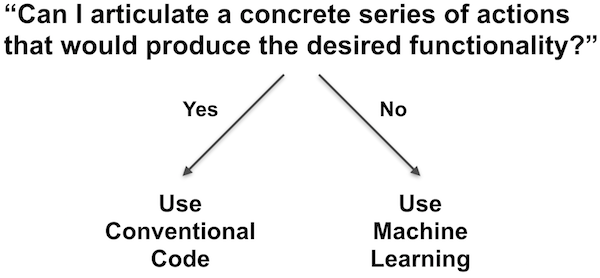
As an introduction to ML this post will walk through how to build a single layer perceptron in Ruby. The perceptron was one of the first functional ML algorithms. It was developed by Frank Rosenblatt in 1957 and was used to build a machine that could identify certain objects. At the time Rosenblatt stated that the “perceptron [is] “the embryo of an electronic computer that [the Navy] expects will be able to walk, talk, see, write, reproduce itself and be conscious of its existence.”
I am far from an expert in this field but luckily perceptrons are relatively straight forward models to build. I have seen them written in python, Java, and javascript but had a hard time finding a ruby version. Attempting to build this out in ruby seemed like a decent contribution that I could make.
Using a common biological analogy, a perceptron is like a single neuron in a larger brain. It is designed to take in inputs and based on those inputs generate an output for other neurons.


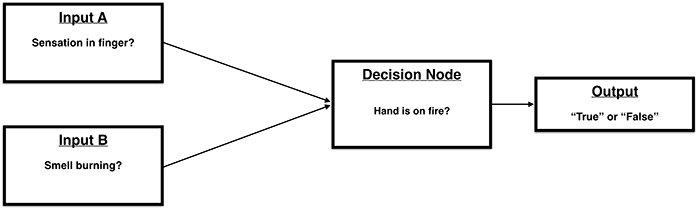
The basic procedure that a perceptron follows is:
- Take in input values; such as X,Y,Z coordinates
- Multiply these values by their respective “weights”. (The appropriate value for these weights is what is being “learned”. They are typically random when initialized)
- Sum all weighted values
- Pass this sum into a function that returns either a 1(true) or 0(false).
The perceptron first goes through a training process where data is passed through with a known “correct” output. As the training data is passed through the weights are adjusted until the inputs produce the correct outputs with a reasonably high success rate. Following this training process the perceptron can then take in new data without a known output and predict the correct output.
To make my own perceptron I followed along with this video in python and translated to ruby as best I could.
The code:
# Original Python code https://github.com/bfaure/AI_Project_4/blob/master/Question_4/main.py#L12
def main
# Bias, x, y, expected output]
data = [[1.00, 0.08, 0.72, 1.0],
[1.00, 0.10, 1.00, 0.0],
[1.00, 0.26, 0.58, 1.0],
[1.00, 0.35, 0.95, 0.0],
[1.00, 0.45, 0.15, 1.0],
[1.00, 0.60, 0.30, 1.0],
[1.00, 0.70, 0.65, 0.0],
[1.00, 0.92, 0.45, 0.0],
[1.00, 0.93, 0.46, 0.0],
[1.00, 0.09, 0.72, 1.0],
[1.00, 0.10, 0.73, 1.0]]
# initial weights
weights = [0.20, 1.00, -1.00]
train_weights(data, weights, 50, 0.5, false, true, false)
end
def predict(inputs, weights)
threshold = 0.0
total_activation = 0.0
weights.zip(inputs).each do |weight, input|
total_activation = input * weight
end
total_activation >= threshold ? 1.0 : 0
end
def accuracy(matrix,weights)
num_correct=0.00
preds = []
mat_len = matrix.size
i = 0
while i < mat_len
# get prediciton
pred = predict(matrix[i][0...-1],weights)
preds << pred
#check accuracy of prediciton
if pred == matrix[i][-1] then num_correct+=1.0 end
i += 1
end
puts "Predictions: #{preds}"
#return overall prediction accuracy
puts "HIII #{num_correct}, #{matrix.size.to_f}"
num_correct/matrix.size.to_f
end
#train the perceptron on the data from the matrix
# trained weights are returned at the end of this function
def train_weights(matrix, weights, nb_epoch = 10, l_rate = 1.0, do_plot = false, stop_early = true, verbose = true)
#iterate over the number of epochs
nb_epoch.times do
#calculate accuracy
cur_acc = accuracy(matrix,weights)
puts "Weights: #{weights}"
puts "Accuracy: #{cur_acc}"
#check if we are done
if cur_acc == 1.0 and stop_early then break end
#iterate over training data
i = 0
while i < matrix.size
prediciton = predict(matrix[i][0...-1],weights)
error = matrix[i][-1]-prediciton
if verbose then puts "Training on data index #{i}" end
#iterate over each weight and update it
j = 0
while j < weights.size
if verbose then puts "\tWeight #{j}" end
weights[j]=weights[j]+(l_rate*error*matrix[i][j])
j += 1
end
i += 1
end
weights
end
end
main
At this point the code could certainly be improved but seems to work on some level. As I tested it I found the weights being slowly adjusted but never saw the accuracy change. I think there may be a problem, either in the text output or with how I’m storing the variables. Currently it predicts a single output for all input data which is not how its supposed to work. I may also take some time to refactor the loops, since I converted them from python in a very simplistic way.
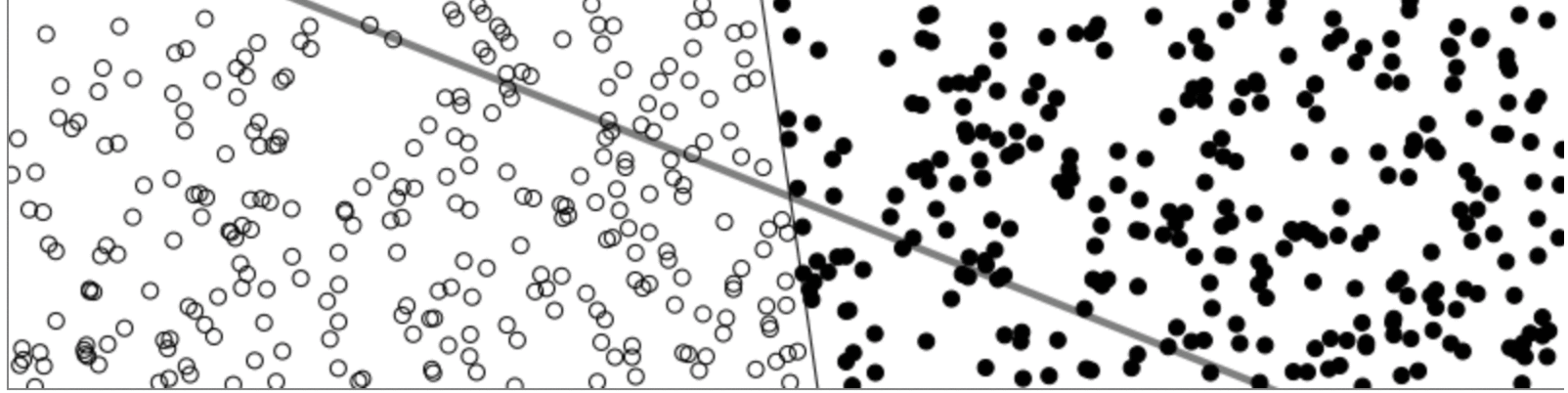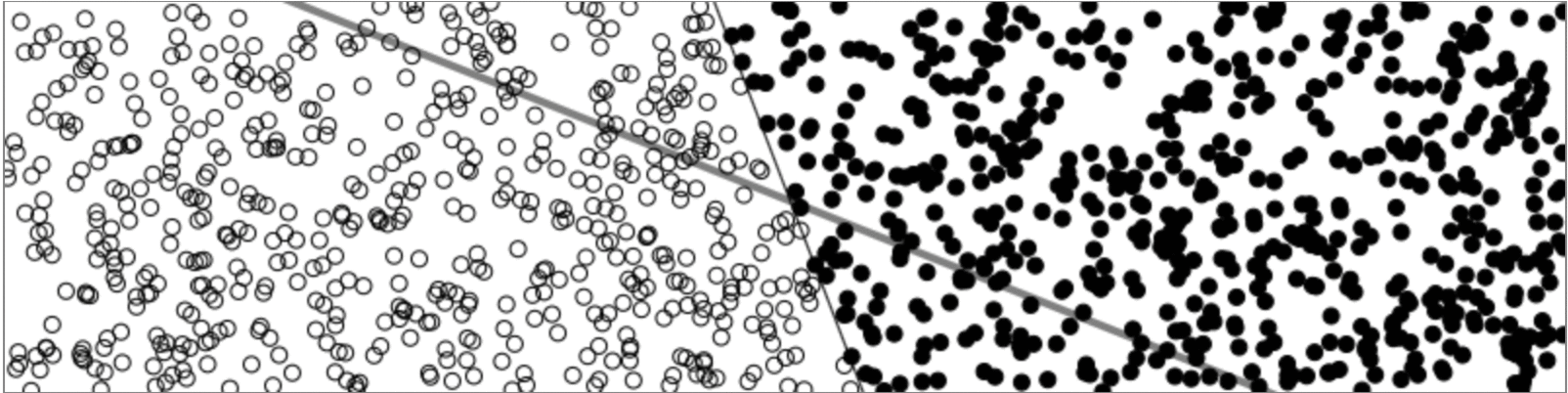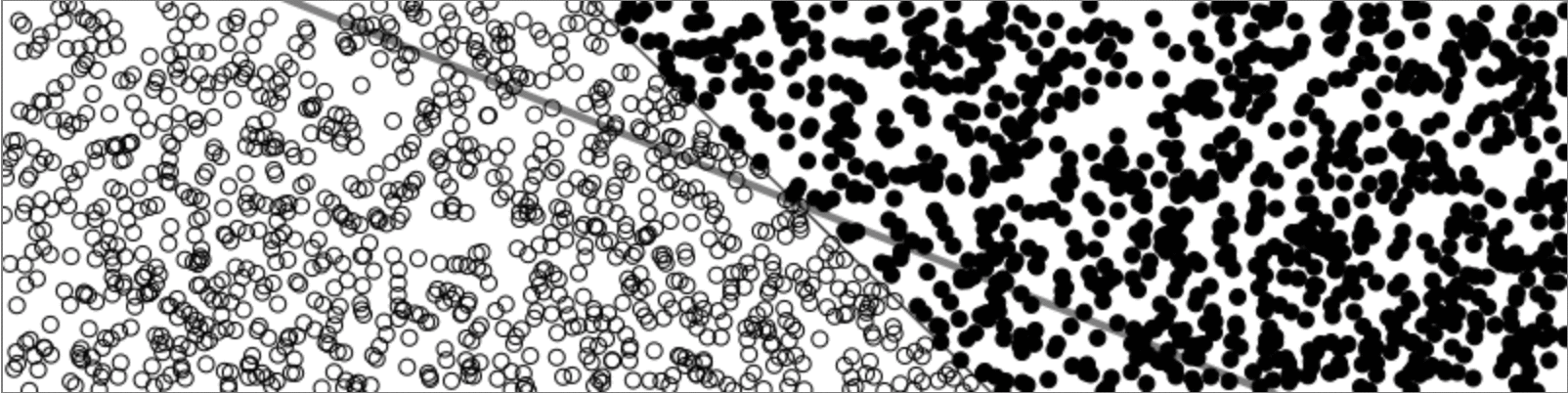
Now, lets say I got this thing working perfectly. It seems relatively simple for a “Machine Learning Algorithm” right? Well it is. It turns out that a perceptron is about as useful as an IF statment. The major failing of a perceptron is that it can only solve “linearly separable problems”. Meaning that if the difference between two groups of data can’t be defined by a line a perceptron will fail. This is also known as a XOR (exclusive OR) problem.
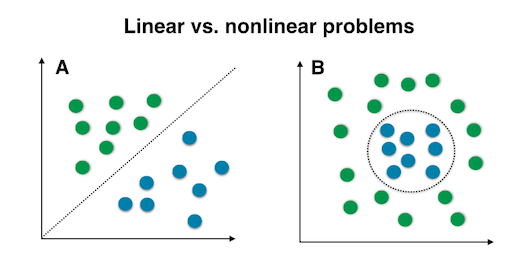
This XOR problem with perceptrons was a major blow to the field and its discovery caused an “AI winter” in which there was little AI/ML funding to be found. However, it was quickly determined that chaining multiple perceptrons together by adding “hidden layers” could solve this XOR problem. Thus the perceptron, while limited, represents a fundamental building block in ML that has been expanded on to produce terrifying, brilliant and powerful software.
Please see these sources for more information. Much of what I wrote about here comes from Patrick Hebron’s Learning Machines class taught at ITP (NYU) and his syllabus (below) provides a great intro for newbies. In addition another(!) ITP professor has made a series of videos on the subject. Its funny, and provides a much better tutorial than I did 🙂.